L'Explosion des Maths - 2002
 La SMF et la SMAI ont réalisé en juillet 2002 une brochure intitulée "L'explosion des mathématiques". Cette initiative de promotion des mathématiques, a été lancée il y a deux ans et a reçu le soutien financier du Ministère de la Recherche et du Comité National Français des Mathématiciens. Elle a bénéficié de la collaboration de nombreux collègues et a pour but de montrer à un large public l'intérêt et la modernité des mathématiques, et d'expliquer les enjeux de la recherche.
La SMF et la SMAI ont réalisé en juillet 2002 une brochure intitulée "L'explosion des mathématiques". Cette initiative de promotion des mathématiques, a été lancée il y a deux ans et a reçu le soutien financier du Ministère de la Recherche et du Comité National Français des Mathématiciens. Elle a bénéficié de la collaboration de nombreux collègues et a pour but de montrer à un large public l'intérêt et la modernité des mathématiques, et d'expliquer les enjeux de la recherche.
Avant-propos - Mireille Martin-Deschamps et Patrick Le Tallec (format pdf 35 ko)
Le temps qu'il fera - Claude Basdevant (format pdf 200 ko) La prévision météorologique ou climatique n'est pas une mince affaire. Elle implique la modélisation de nombreux phénomènes de natures différentes, et l'intervention de plusieurs sciences, des mathématiques à la biologie, en passant par l'informatique, la physique ou la chimie.
Les dessous du téléphone portable - Daniel Krob (format pdf 512 ko) Le téléphone mobile est maintenant un objet relativement banal. Qui n'a jamais vu un portable ou téléphoné avec ? Mais rares sont ceux qui ont une pensée pour la science et la technologie mises en jeu.
Cryptage et décryptage : communiquer en toute sécurité - Jean-Louis Nicolas (format pdf 169 ko) Dans le monde actuel, où les télécommunications occupent une place cruciale, la cryptographie est un enjeu majeur. Elle est aussi devenue une science complexe, qui ne peut se passer de mathématiciens de haut niveau.
Contrôler un monde complexe - Pierre Perrier (format pdf 232 ko) Qu'il s'agisse de la manœuvrabilité d'un avion, de la tenue mécanique d'une structure compliquée ou de la gestion du trafic automobile, le progrès dans ces domaines ne vient pas uniquement des inventions purement techniques. Il naît aussi de recherches abstraites, comme la théorie mathématique du contrôle.
Le théorème du soufflet - Étienne Ghys (format pdf 192 ko) Une règle, un crayon, du carton, des ciseaux et de la colle : il n'en faut guère plus pour procurer aux mathématiciens du plaisir et de jolis problèmes - dont l'étude se révèle souvent, après coup et de manière inattendue, utile dans d'autres métiers.
Trouver un gène responsable de cancer - Bernard Prum (format pdf 104 ko) Les développements de la biologie moderne, et notamment ceux de la génétique moléculaire, exigent de nouveaux outils mathématiques. Exemple avec la statistique et son rôle dans la recherche d'un gène lié au cancer du sein.
Des ondelettes pour comprimer une image - Stéphane Mallat (format pdf 122 ko) Qu'elles soient stockées numériquement dans des mémoires informatiques ou qu'elles voyagent à travers Internet, les images occupent beaucoup de place. Heureusement, il est possible de les « condenser » sans altérer leur qualité !
Empêcher les ondes de faire du bruit - Daniel Bouche (format pdf 165 ko) Comment échapper à la détection par un radar ? Quelle est la forme optimale d'un mur anti-bruit ? Peut-on améliorer les images échographiques ? Pour recevoir une réponse satisfaisante, ces questions demandent des analyses théoriques poussées.
Quand art rime avec maths - Francine Delmer (format pdf 286 ko) Les mathématiques n'inspirent pas que les scientifiques. De nombreux artistes y ont puisé la matière de certaines de leurs œuvres. La réciproque est parfois vraie aussi, comme dans le cas de la perspective, où l'art a montré le chemin à des théories géométriques.
De l'ADN à la théorie des nœuds - Nguyen Cam Chi et Hoang Ngoc Minh (format pdf 188 ko) L'activité biologique de la molécule d'ADN dépend notamment de son agencement dans l'espace et de la façon dont elle est entortillée - choses qui sont du ressort de la théorie mathématique des nœuds.
Le philosophe et le mathématicien - Pierre Cassou-Noguès (format pdf 344 ko) Tout au long de leur histoire, la philosophie et les mathématiques ont entretenu une relation aussi étroite qu'énigmatique. Il faudrait revenir à Platon dans le monde grec et à Descartes à l'aube de l'époque moderne. Évoquons ici deux grandes figures du XXe siècle, David Hilbert et Edmund Husserl.
Comment rationaliser les ventes aux enchères ? - Jean-Jacques Laffont (format pdf 327 ko) Grâce notamment à Internet, les ventes aux enchères se généralisent. La modélisation de ces procédés de vente permet de définir les règles et stratégies optimales de leur utilisation.
De l'économétrie pour vendre des vins ou des obligations - Philippe Février et Michael Visser (format pdf 181 ko) Grands vins ou bons du Trésor font l'objet de ventes aux enchères. Mais quel type d'enchères faut-il pratiquer ? Pour le savoir, on complète les modélisations générales des enchères par des études économétriques.
Les casse-tête des compagnies aériennes - Jean-Christophe Culioli (format pdf 124 ko) Les problèmes d'organisation et de planification posés à une compagnie aérienne sont analogues à ceux rencontrés dans d'autres secteurs d'activité. La recherche opérationnelle, domaine qui concerne des dizaines de milliers de mathématiciens et d'ingénieurs dans le monde, s'évertue à les résoudre au mieux.
De la géométrie à 11 dimensions pour comprendre la Genèse ? - Maurice Mashaal (format pdf 239 ko) Les physiciens aspirent depuis longtemps à une théorie capable d'englober toutes les particules élémentaires et toutes leurs interactions. Depuis une quinzaine d'années, ils ont une piste sérieuse. Pour l'explorer, ils doivent naviguer dans des espaces hautement abstraits où même les mathématiciens ne s'étaient pas encore aventurés.
Internet : modéliser le trafic pour mieux le gérer - François Baccelli (format pdf 298 ko) Les spécialistes des réseaux de communication s'efforcent de bien comprendre les propriétés statistiques du trafic de données qu'ils doivent acheminer. La gestion de ces réseaux et leur développement en dépendent.
Le prix des options financières - Elyès Jouini (format pdf 143 ko) Le monde de la finance fixe le prix des options au moyen de formules qui ont été obtenues grâce à des travaux mathématiques relativement récents. La recherche de meilleures formules se poursuit... et cela ne concerne pas que les boursicoteurs !
Communiquer sans erreurs : les codes correcteurs - Gilles Lachaud (format pdf 202 ko) Pour détecter et corriger les inévitables erreurs qui affectent les échanges d'information numérisée, les spécialistes du codage numérique en appellent à des méthodes abstraites qui relèvent de l'algèbre ou de la géométrie.
Reconstruire des surfaces pour l'imagerie - Jean-Daniel Boissonnat (format pdf 176 ko) Reconstituer une surface en ne connaissant que certains de ses points : un problème que l'on rencontre souvent, qu'il s'agisse d'exploration géologique, d'archivage de vestiges archéologiques, d'imagerie médicale ou industrielle.
Les mathématiciens en France et dans le monde - Jean-Pierre Bourguignon (format pdf 244 ko) Jusque vers la fin du XIXe siècle, les « géomètres », comme on appelait jadis les mathématiciens, étaient peu nombreux. En un siècle, leurs rangs se sont considérablement renforcés. Aujourd'hui, ils doivent faire face à une profonde mutation de leur discipline.
Comment devenir mathématicien ? - Maurice Mashaal (format pdf 227 ko) De longues années d'apprentissage et des talents évidents sont nécessaires pour qui veut faire de la recherche fondamentale en mathématiques. Mais les passionnés ont à leur disposition plusieurs filières de formation, avec des débouchés variés.
Mathématiques: l'Explosion continue... (2013)
La brochure « Mathématiques, l'explosion continue », conçue par la Fondation Sciences Mathématiques de Paris (FSMP), la Société Française de Statistiques (SFdS), la Société de Mathématiques Appliquées et Industrielles (SMAI) et la Société Mathématique de France (SMF), a été réalisée grâce au soutien financier de Cap'Maths.
Les 25 chapitres et l'avant-propos (du premier au dernier)
 |
Avant-propos Maria J. Esteban, présidente de la Société de Mathématiques Appliquées et Industrielles (2009-2012), Bernard Helffer, président de la Société Mathématique de France (2010-2012), Jean-Michel Poggi, président de la Société Française de Statistique (2011-2013) |
 |
Couper, attendrir, trancher, réduire : un conte culinaire sur la résolution informatique des problèmes difficiles Nicolas Schabanel, directeur de recherche CNRS à l'Université Paris Diderot, Pierre Pansu, professeur à l'Université Paris-Sud Comment répartir ses invités sur deux tablées sans placer ensemble ceux qui se détestent ? Résoudre ce casse-tête quel que soit le nombre d'invités est un problème informatique extrêmement difficile à resoudre quand le nombre d’invités augmente. A l'aide d'un peu de programmation géométrique, on peut trouver une réponse approchée de garantie présumée optimale. |
 |
Garder le contrôle... à l'aide des mathématiques Karine Beauchard, chargée de recherche CNRS à l'École polytechnique, Jean-Michel Coron, professeur à l'Université Pierre et Marie Curie, Pierre Rouchon, professeur à Mines-ParisTech Contraindre la trajectoire d'un satellite, réguler la température de sa maison, stabiliser le niveau d'eau d'un canal... les situations nécessitant que l'on contrôle une donnée, une quantité, une position, sont omniprésentes. Ces problèmes sont l'objet d'une théorie mathématique très riche: la théorie du contrôle. |
 |
Le théorème de Green-Tao et autres secrets des nombres premiers Michel Waldschmidt, professeur émérite à l'Université Pierre et Marie Curie Bien que les mathématiciens s'y intéressent depuis l'Antiquité, les nombres premiers continuent de fasciner. En les additionnant ou en les soustrayant entre eux, on trouve une mine de problèmes dont certains sont longtemps demeurés ouverts ou restent encore irrésolus. |
 |
La supraconductivité Sylvia Serfaty, professeur à l'Université Pierre et Marie Curie La supraconductivité, capacité d'un métal à laisser passer le courant électrique sans perte d'énergie, peut avoir des applications étonnantes. L'étude de ce phénomène fait intervenir divers domaines des mathématiques, comme le calcul des variations, les équations aux dérivées partielles, l'analyse asymptotique. Plusieurs questions ouvertes y sont associées. |
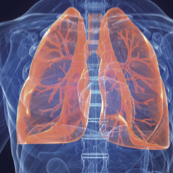 |
Inspiration mathématique : la modélisation du poumon Céline Grandmont, directrice de recherche à Inria La complexité de notre système respiratoire en fait un joli sujet d'application des mathématiques. Le fonctionnement de l'appareil respiratoire est décrit par des équations qui servent à effectuer des simulations venant compléter l'expérience et permettant de mieux comprendre ou prévoir les phénomènes qui se produisent lorsque nous respirons. |
 |
Le temps qu'il fera Claude Basdevant, professeur à l'Université Paris 13 et à l'École polytechnique La prévision météorologique ou climatique n'est pas une mince affaire. Elle implique la modélisation de nombreux phénomènes de natures différentes et l'intervention de plusieurs sciences, des mathématiques à la biologie, en passant par l'informatique, la physique ou la chimie. |
 |
Internet, feux de forêt et porosité : trouvez le point commun Marie Théret, maître de conférences à l'Université Paris Diderot Echanges de données entre internautes, propagation d'un feu de forêt, infiltration de l'eau dans une roche : un modèle mathématique simple utilisant des graphes permet de mieux comprendre ces phénomènes. |
 |
À la recherche de la forme idéale Grégoire Allaire, professeur à l'École polytechnique, François Jouve, professeur à l'Université Paris Diderot Les objets issus de la fabrication industrielle sont pensés de façon à optimiser un certain nombre de paramètres comme le poids ou la solidité. Pour éviter de chercher à tâtons la meilleure forme possible, on peut aujourd'hui compter sur plusieurs méthodes mathématiques d'optimisation. |
 |
La biodiversité mise en équations... ou presque Sylvie Méléard, professeur à l'École polytechnique Prédire l'évolution d'une population animale sur une longue période, connaître le fonctionnement d'un écosystème, comprendre l'avantage de la reproduction sexuée pour la survie des espèces... les problèmes issus de la biodiversité sont complexes et leur résolution fait appel à des outils mathématiques sophistiqués. |
 |
La restauration de vieux films Julie Delon, chargée de recherche à Telecom ParisTech, Agnès Desolneux, directrice de recherche CNRS à l'École Normale Supérieure de Cachan Le papillonnage fait partie des défauts qui affectent couramment les bandes abîmées. À travers ce cas particulier, voyons comment les mathématiques aident à créer des algorithmes permettant de corriger automatiquement les imperfections des vieux films. |
 |
Cryptage et décryptage : communiquer en toute sécurité Jean-Louis Nicolas, professeur à l'Université Claude Bernard Lyon 1, Christophe Delaunay, professeur à l'Université de Franche-Comté La sécurisation de nos cartes bleues, ainsi que d'autres procédés de cryptages uti- lisés couramment, se basent sur l'impossibilité, en pratique, de factoriser de très grands nombres. Ce type de cryptage pourrait cependant être détrôné par d'autres méthodes, sa fiabilité étant sans cesse remise en question par les progrès de l'informatique. |
 |
Pourquoi et comment nager dans le miel ? François Alouges, Guilhem Blanchard, Sylvain Calisti, Simon Calvet, Paul Fourment, Christian Glusa, Romain Leblanc et MarioQuillas-Saavedra, respectivement professeur et élèves de l'École polytechnique La nage dans des milieux très visqueux comme le miel est un sujet de recherches actuel, qui touche des disciplines aussi diverses que la mécanique des fluides, les mathématiques appliquées ou la biologie. Mais pourquoi donc s'intéresser à la natation dans du miel? Et quelles sont les différences entre la nage dans du miel et celle dans de l'eau? |
 |
Le théorème du soufflet Étienne Ghys, directeur de recherche CNRS à l'École Normale Supérieure de Lyon Une règle, un crayon, du carton, des ciseaux et de la colle: il n'en faut guère plus pour procurer aux mathématiciens du plaisir et de jolis problèmes - dont l'étude se révèle souvent, après coup et de manière inattendue, utile dans d'autres métiers. |
 |
La détection de spams : un jeu d'enfant ? Tristan Mary-Huard, chargé de recherche Inra à Inra-AgroParisTech Comment distinguer automatiquement un spam d'un message normal ? Les filtres anti-spams analysent le texte des messages en utilisant des algorithmes de classification en forme d'arbres. Ceux-ci comportent un nombre optimal de nÅ“uds correspondant à autant de questions pertinentes permettant de déterminer la nature d'un message. |
 |
L'art de couper les têtes sans faire mal Erwan Le Pennec, chargé de recherche Inria à l'Université Paris-Sud Le principe du scanner implique de savoir retrouver un objet à partir d'une collection de radiographies de cet objet. Il s'agit de ce que l'on appelle, en mathématiques, un problème inverse. Sa résolution s'avère difficile et constitue toujours une source de questions pour les mathématiciens. |
 |
Climatologie et statistiques Pascal Yiou, directeur de recherche au CEA, Philippe Naveau, chargé de recherche CNRS à l'Institut Pierre Simon Laplace L'étude du climat et de ses variations est basée sur un grand nombre d'outils et concepts statistiques. Ceci se reflète dans le langage employé par les différents rapports du GIEC (Groupe International d'Experts sur le Climat), qui mettent beaucoup l'accent sur les incertitudes et leur quantification. |
 |
Chercher sur le Web : juste un point fixe et quelques algorithmes Serge Abiteboul, directeur de recherche Inria à l'École Normale Supérieure de Cachan Le Web met à notre disposition une masse considérable d'information, plusieurs dizaines de milliards de documents. Sans les moteurs de recherche, ces systèmes de plus en plus sophistiqués qui nous aident à nous focaliser sur un petit nombre de pages, le Web ne serait qu'une poubelle à ciel ouvert, gigantesque et inutilisable. Le rôle de ces systèmes est de faire surgir de la masse des internautes une intelligence collective pour évaluer, classer, filtrer les informations. Comment les moteurs de recherche gèrent-ils ces volumes d'information véritablement phénoménaux? Comment aident-ils les utilisateurs à trouver ce qu'ils cherchent dans cette masse ? Retour sur un des plus beaux succès du Web. |
 |
La brouette de Monge ou le transport optimal Yann Brenier, directeur de recherche CNRS à l'École polytechnique Né d'un problème concret - comment déplacer au mieux un tas de sable - le transport optimal est un outil qui trouve des applications aussi bien à l'intérieur des mathématiques (de la géométrie à l'analyse fonctionnelle) que dans d'autres domaines, comme la gestion de ressources, par exemple. |
 |
Des statistiques pour détecter les altérations chromosomiques Emilie Lebarbier, maître de conférences, Stéphane Robin, directeur de recherche Inra à AgroParisTech Les altérations chromosomiques sont responsables de nombreuses maladies, parmi lesquelles certains cancers. La détection de petites altérations, essentielle pour le diagnostic du médecin, fait appel à un modèle classique en statistiques: la segmentation. |
 |
Le piano rêvé des mathématiciens Juliette Chabassier, chargée de recherche, équipe Magique - 3D, Inria Comme de nombreux phénomènes physiques, le fonctionnement d'un piano peut être modélisé grâce aux mathématiques. Mais le modèle obtenu permet aussi d'aller plus loin, de rêver de pianos impossibles ou d'imaginer des sons nouveaux. La recherche offre ainsi au compositeur un formidable champ d'exploration et de création. |
 |
Comment faire coopérer des individus égoïstes ? Yannick Viossat, maître de conférences à l'Université Paris-Dauphine La coopération est au coeur de nombreux comportements sociaux ou biologiques. La théorie des jeux permet d'expliquer le choix de stratégies coopératives et d'en comprendre les mécanismes dans des contextes où les individus se trouvent en concurrence, des situations de guerre à la régulation de la pêche. |
 |
AVC : les mathématiques à la rescousse Emmanuel Grenier, professeur à l'École Normale Supérieure de Lyon L'AVC, qui touche des milliers de personnes chaque année, est une pathologie complexe dont le diagnostic et le traitement nécessitent encore d'être améliorés. C'est un des domaines où la modélisation mathématique peut venir en aide à la recherche médicale, en complétant notamment l'expérimentation sur les animaux. |
 |
Point de vue sur les mathématiques françaises depuis l'étranger John Ball, professeur à l'Université d'Oxford Les mathématiques françaises ont la réputation d'être parmi les meilleures au monde. Qu'est-ce qui explique leur exceptionnelle qualité ? Voici un décryptage de cette particularité hexagonale à travers le regard du mathématicien britannique John Ball. |
 |
EDP à la française John Ball, professeur à l'Université d'Oxford Spécialiste des équations aux dérivées partielles, John Ball raconte ici comment ce domaine des mathématiques appliquées a connu un formidable essor en France, grâce en particulier à une figure emblématique: le professeur Jacques- Louis Lions. |
 |
F.A.Q. (et idées reçues) sur les mathématiciens Quels sont les débouchés des cursus de mathématiques? Comment devient-on mathématicien(ne)? En quoi consiste ce métier? Des professionnels, hommes et femmes, répondent à ces questions et tordent le cou aux idées reçues. |